In den Jahren 1966 und 1967 fand Frans Fransson heraus, dass die Anregungsfunktion von Doppelrohrblattinstrumenten auch als eine Folge von Druckimpulsen interpretiert werden kann, die den Verlauf des Klangspektrums prägt (Fransson 1966; Fransson 1967): Je nach Anordnung der Druckimpulse bilden sich Minima im Spektrum aus, zwischen denen sich formantähnliche Zonen ausbreiten.
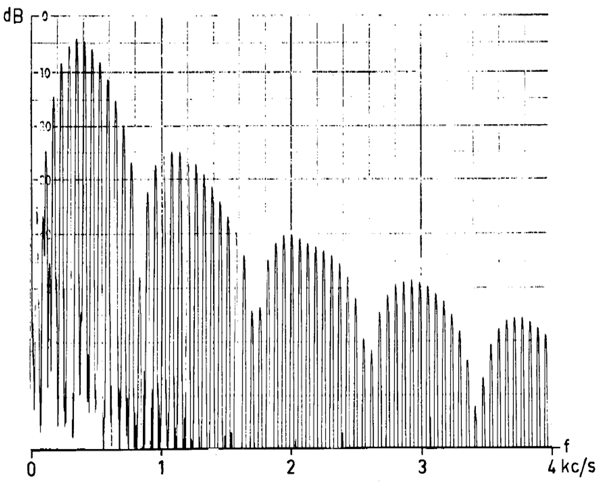
Quellenstrecken mit typischen Formantbereichen für das Fagott
(Fransson 1966)
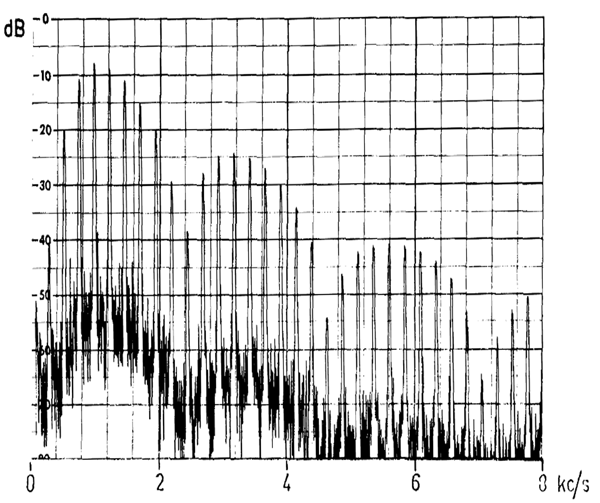
Quellenstrecken mit typischen Formantbereichen für die Oboe
(Fransson 1967)
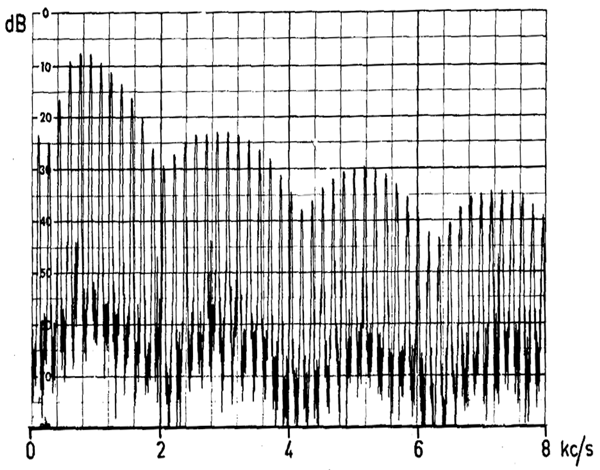 Quellenstrecken
mit typischen Formantbereichen für das English Horn
Quellenstrecken
mit typischen Formantbereichen für das English Horn
(Fransson 1967)
(Formantstrecken = feststehende Bereiche innerhalb des Klangspektrums, in denen die Teiltöne unabhängig von der Grundtonhöhe in ihrer Amplitude hervorgehoben werden. Diese hervorgehobenen Teiltonbereiche im Spektrum rufen die Klangfarbenempfindung des jeweiligen Instrumentes hervor).
Die Klänge von Blasinstrumenten scheinen nach dieser Gesetzmäßigkeit der Impulsformung gebildet zu werden. Seine charakteristische Klangfarbe erhält das Instrument durch die Form der Impulsfolgen. Diese Folgen von Impulsen entstehen in den Originalinstrumenten durch die Ventilfunktion des Rohrblattes oder der Lippen: In gleichen Abständen treten die Impulse durch die Lippen oder durch das Rohrblatt/Doppelrohrblatt in den angeschlossenen Hohlraum und regen diesen zum Schwingen an.
Messung der Rohrblatt-Öffnungs- und -Schließzeiten beim Fagott (Voigt 1975):
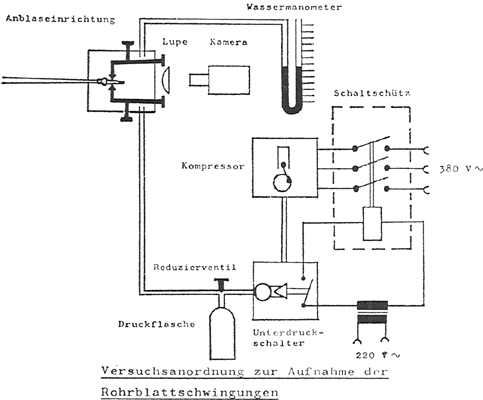
Versuchsaufbau zur Aufnahme der Rohrblattschwingungen
(Voigt 1975)

Filmaufnahmen (1000 Bilder/Sekunde) der Rohrblattschwingung
(Voigt 1975)
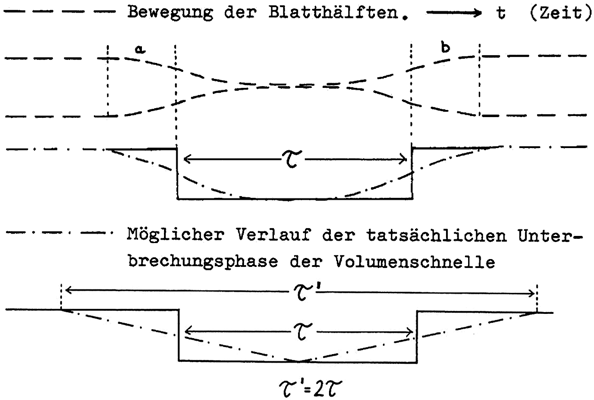
Cosinusförmige Schließzeit der Rohrblätter, Annäherung
an eine Rechteckschwingung
(Voigt 1975)
Das stetige Öffnen und Schließen der Rohrblätter oder Lippen wird bei der Impulsformung elektronisch nachgebildet, indem an die Stelle der kurzfristigen Lippen- oder Rohrblattöffnung der elektronische Impuls gesetzt wird.
Nach der Theorie der Entstehung zyklischer Spektren durch Impulsfolgen gibt es dafür folgende Gesetze:
Wie oben schon ausgeführt ist die grundlegende Bedingung für feste
Formanten eine konstante Öffnungs- und Verschlußzeit bei veränderbarer
Impulsfrequenz. Das heißt: Egal wie schnell die Impulsfolge ist,
also welche Frequenz sie hat, muß die Breite der Impulse konstant
gehalten werden. Wird die Impulsbreite nur geringfügig verändert,
zieht diese Veränderung die feinmodulatorischen Vorgänge in
der Klangfarbe nach sich, wie man sie auch bei Original-Blasinstrumenten
gewohnt ist. Mit anderen Worten: Je konstanter die Impulsbreite, desto
konstanter ist die Verteilung der Teiltonminima im Spektrum. Minimale
Veränderungen der Impulsbreite bewirken hörbare Veränderungen
im Spektrum.
Dabei gilt: Bei einer Impulsbreite von t liegen die Minima im Spektrum
in den Teiltonabständen von 1/t (oder 1/T-t, wenn die konstante Periode
T-t kleiner oder gleich der Periode T ist). (Dies entspricht dem Schumannschen
Formantstreckengesetz).
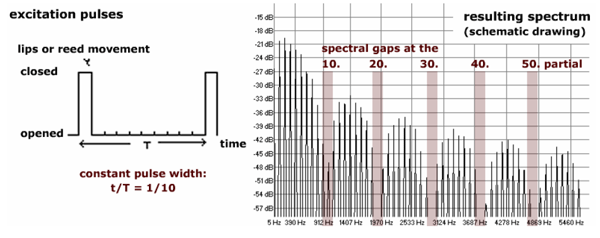 Impulsfolge und Spektrum (t/T = 1/10)
Impulsfolge und Spektrum (t/T = 1/10)
(Oehler, Reuter 2005)
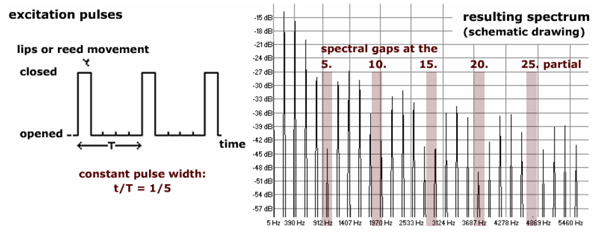 Impulsfolge und Spektrum (t/T = 1/5)
Impulsfolge und Spektrum (t/T = 1/5)
(Oehler, Reuter 2005)
Bei p-Klängen wird die Impulsform abgerundeter. Dies bedeutet für das Spektrum, daß die höheren Teiltöne schwächer ausgeprägt sind als normal. Bei f-Klängen wird die Impulsform kantiger. Dies bedeutet für das Spektrum, daß die höheren Teiltöne stärker ausgeprägt sind als normal. Mit anderen Worten: Je kantiger die Impulsform, desto stärker sind die höheren Teiltöne im Spektrum vertreten.
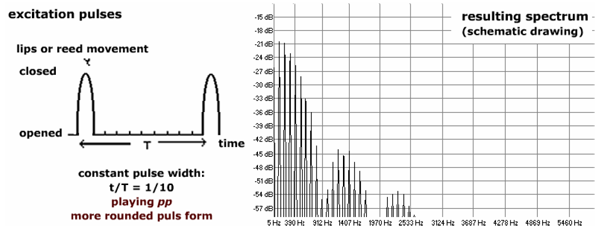
abgerundete Impulsfolge und ihr Spektrum (im pp)
(Oehler, Reuter 2005)
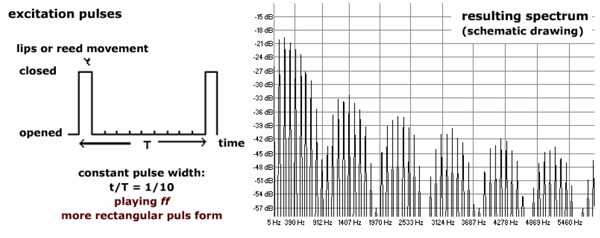
kantige Impulsfolge und ihr Spektrum (im pp)
(Oehler, Reuter 2005)
Bei einer minimalen Verkürzung der Impulszeiten werden die Minima im Spektrum und die dazwischen liegenden Formantbereiche nach oben hin verschoben, ohne daß die Teiltöne mitwandern. Das Teiltonmaximum verschiebt sich also nach oben, vorher leisere Teiltöne werden hervorgehoben (Dies entspricht dem Schumannschen Formantverschiebungsgesetz).
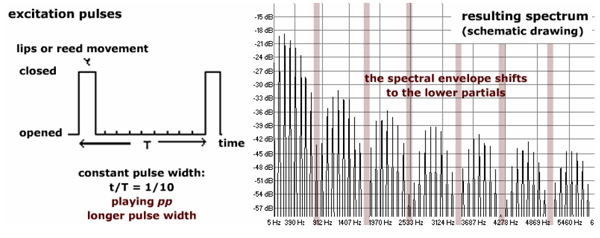
breitere Impulsweite im pp führt zu kürzeren Abständen
zwischen den spektralen Lücken
(Oehler, Reuter 2005)
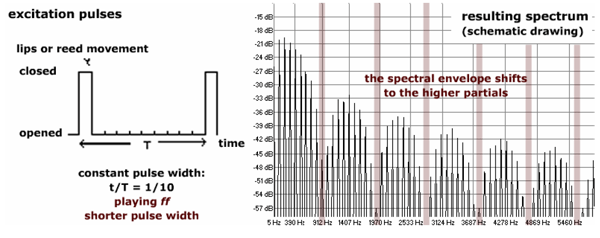
schmalere Impulsweite im ff führt zu weiteren Abständen zwischen
den spektralen Lücken
(Oehler, Reuter 2005)
Der Impulsformung des Variophons und der Martinetta liegen Rechteckimpulse zugrunde. Überträgt man dieses Modell aber auf die Anregungsfunktion echter Blasinstrumente, so steht man vor dem Problem, daß der Rechteckimpuls nur entstehen kann, wenn die Öffnungs- und Schließzeiten der Rohrblätter/ Lippen als unendlich klein angenommen werden. Dies ist aber nicht der Fall: Zwischen dem Zustand "Auf" und "Zu" vergeht eben immer eine kurze Zeit, so daß man Dreiecks- oder Cosinusimpulsfolgen als Anregungsfunktion für Blasinstrumente annehmen muß.
Bei der Bildung des Spektrums aus Dreiecksimpulsen gelten folgende Gesetzmäßigkeiten:
Die Verteilung der Minima im Klangspektrum hängt nun von der Auf- und Abstiegszeit (t1 und t2-t1) des Dreiecksimpulses (t2) innerhalb der Periode (T) ab: Solange die Abstiegszeit (t2-t1) zum Gesamtimpuls in einem ganzzahligen Verhältnis steht und solange das Teilungsverhältnis zwischen der Auf- und Abstiegszeit (t1 und t2-t1) konstant bleibt, bleibt die Position der Minima und der dazwischen liegenden Formantstrecken konstant.
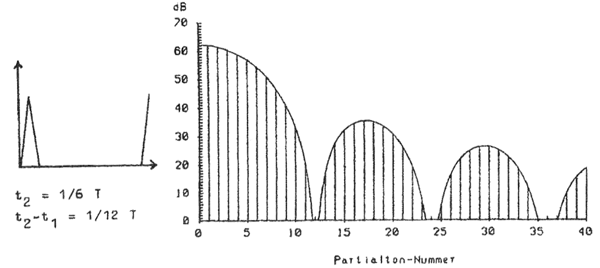
Dreiecksimpulsfolge und ihr Spektrum (t2 = 1/6 T und t2-t1 = 1/12
T)
(Auhagen 1987)
Dabei bestimmt das Verhältnis von der Abstiegsflanke (t2-t1) zur Periode (T) die auch von den Rechteckimpulsen bekannten Oberzyklen, während das Verhältnis der Aufstiegsflanke (t1) zur Periode (T) die Ursache für die Unterzyklen im Spektrum ist.
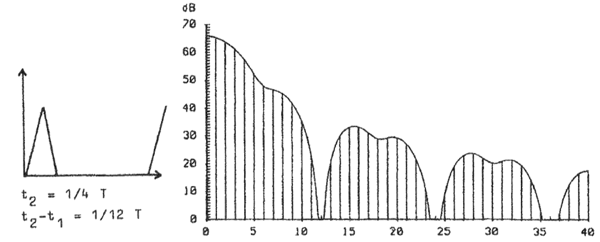 Dreiecksimpulsfolge und ihr Spektrum (t2 = 1/4 T und t2-t1 = 1/12
T)
Dreiecksimpulsfolge und ihr Spektrum (t2 = 1/4 T und t2-t1 = 1/12
T) (Auhagen 1987)
Die Gesetzmäßigkeiten für die Spektren von Cosinus- und
zusammengesetzten Impulsen sind noch ein wenig komplexer und werden in
den Arbeiten von Blens (1993), Fricke & Blens (1994), Baumgartner
(2012) und Gadermaier (2013) beschrieben.


